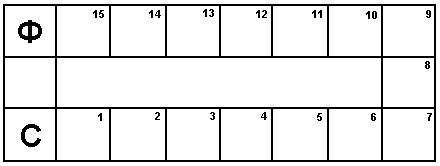
Вероятности в "норильской" игре

Представьте, что несколько человек играют в следующую игру. Каждый игрок размещает фишку на поле, обозначенной буквой «С».

Каждый раз в свой ход игрок бросает кубик – 1D6 – шестигранный кубик, на гранях которого нанесены 1, 2, 3, 4, 5 и 6 точек. В зависимости от выпавшего на верхней грани числа игрок перемещает свою фишку против часовой стрелки на такое же число полей.

Игрок выигрывает тогда, когда при своем очередной ходе он заканчивает перемещение фишки точно на поле, обозначенном буквой «Ф». Если игрок вынужден миновать поле «Ф», то он продолжает двигаться по кругу (против часовой стрелки), вновь и вновь испытывая возможность завершить ход на желаемой клетке.

В усложненной версии игры каждый игрок мог разместить на свободной клетке поля фишку – помощника, который позволял при попадании игрока на данную клетку сделать дополнительный ход (с броском кубика), а при попадании на эту клетку чужого игрока – чужой игрок перемещался на начальную клетку «С».

Фишку-помощника игроки размещают поочередно, при этом нельзя выбирать клетки с «С» и «Ф», а также уже занятые другими фишками.

В связи с этим возникает два вопроса:

• Куда выгоднее размещать фишку первому игроку?
• И какая вероятность оказаться точно на клетке «Ф» с первого раза (на первом кругу)?

Давайте посчитаем.

При первом броске вероятность оказаться на клетке «1» составляет 1/6, на клетках «2», «3», «4», «5», «6» аналогично – 1/6. После второго броска кубика вероятность попадания на клетки перестает быть равной. Дело в том, что к клеткам со «2» по «6» добавляется вероятность попадания на них после того, как фишка оказалась на клетке «1» после первого хода.

После третьего броска некоторые игроки могут уже пойти на второй круг.

Игроки, которые попадают на (или проходят через) «С», платят в общий банк игры ставку. Общий банк забирает игрок, который, все-таки, точно попадет на клетку «Ф».

Здесь стоить заметить, что вероятность нахождения на первых клетках стала отличной от ноля, так как игроки пошли на второй круг. Также, если сложить вероятности нахождения фишки на всех клетках, то получится число меньше 1. Это связано с тем, что из соревнования вычитаются те вероятности, которые выиграли игру, то есть с клетки «Ф» дальнейшего движения фишки не происходит. То есть, если на «15»-клетку можно попасть из шести клеток: «14», «13», «12», «11», «10», «9», то на клетку «без номера» только с пяти клеток: «15», «14», «13», «12», «11».

Вероятность, что игра не закончилась после пятого хода, составляет 82,3%.

Вероятность, что игра не закончилась после шестого хода, составляет 80,6%.

Дальше считать становится не очень интересно, так как уже довольно много чисел.

Ответ на вопрос №1:

Пока ориентировочно видно, что оптимальной точкой для размещения фишки-помощника является клетка под номером «6». Если кто-то хочет опровергнуть это утверждение, то, пожалуйста, продолжайте расчеты.

Ответ на вопрос №2:

Ответ на этот вопрос мне кажется более простым. Так как на первом круге (без фишки-помощника) попасть на клетку «Ф» можно из шести предыдущих клеток, и из каждой этой клетки попасть точно в клетку «Ф» можно только одним значением кубика, то вероятность закончить игру на первом круге всегда будет равна вероятности выпадения одного из шести возможных значений этого кубика, то есть 1/6.

Назад